
Grupo de Física Aplicada, Universidade de Genebra, 1211 Genegra 4, SuíÇA
(3 DE JUNHO DE 2019)
É comum identificar as condições iniciais de sistemas dinâmicos clássicos com números matemáticos reais. No entanto, quase todos os números reais contêm uma quantidade infinita de informação. Eu argumento que um volume finito de espaço não pode conter mais que uma quantidade finita de informação, e que, portanto, os números matemáticos reais não são fisicamente relevantes. Além disso, uma melhor terminologia para os assim chamados números reais é a de “números aleatórios”, visto que suas séries de bits são realmente aleatórias. Proponho uma mecânica clássica alternativa, que é empiricamente equivalente à mecânica clássica, mas usa somente números de informação finita [finite-information numbers]. Essa mecânica clássica alternativa é não-determinística, apesar do uso de equações determinísticas, de modo similar à teoria quântica. É interessante que tanto a mecânica clássica alternativa quanto as teorias quânticas podem ser suplementadas por variáveis adicionais de tal forma que a teoria suplementada é determinística. A maioria dos físicos suplementam diretamente a teoria clássica com números reais aos quais eles atribuem existência física, enquanto a maioria dos físicos rejeita a mecânica bohmiana como teoria quântica suplementada, argumentando que as posições bohmianas não tem realidade física.
I. INTRODUÇÃO
A física é apresentada de forma recorrente como exemplo de uma explicação determinística do nosso mundo. Além disso, é frequentemente argumentado que todas as boas explicações têm de seguir tal estrutura. Isso é comumente ilustrado pela física clássica, uma teoria cujo poder explicativo é realmente impressionante, apesar do fato de que seus limites são bem compreendidos (ou justamente por conta disso?). De fato, o domínio de validade da mecânica clássica é limitado pela relatividade e pela teoria quântica, cujas predições são mais precisas quando velocidade e tamanho (ou ação) se aproximam de valores críticos determinados pelas constantes universais c e ħ, respectivamente.
A mecânica clássica é um conjunto de equações dinâmicas, com as condições iniciais – tipicamente posição e momento de partículas pontuais – dadas por números reais. Exceto em casos particulares[1], essas equações dinâmicas, juntamente com as condições iniciais, determinam completamente e por si mesmas as soluções em todo o tempo futuro e passado. Assim, a conclusão é que a física clássica é determinística.
Isso tem consequências enormes. Primeiro, como já foi dito, isso é frequentemente tomado como a meta de toda boa explicação científica. Por exemplo, muitos filósofos e físicos tentam formular a física quântica de tal modo que se recupere alguma coisa do determinismo clássico, apesar da aleatoriedade quântica; nas seções VII e VIII eu discuto a mecânica bohmiana nesse contexto. Segundo, se o determinismo científico fosse a única boa explicação científica, então seria extremamente tentador concluir que tudo que está – pelo menos em princípio – no escopo da ciência acontece necessariamente, i.e., está determinado desde o big-bang, incluindo todos os processos fisiológicos.
Na minha opinião – mas esse trabalho é independente dessa opinião – isso tem consequências terríveis: nosso mundo seria como um filme dentro de uma caixa fechada sem nenhum espectador. Se esse trabalho for válido, então há uma grande harmonia entre a física e nossa experiência [2].
Na primeira parte desse trabalho eu argumento que há uma outra teoria, parecida mas diferente da mecânica clássica, que tem exatamente o mesmo conjunto de previsões, apesar de essa teoria alternativa ser indeterminística[2]. Em poucas palavras, essa teoria alternativa tem as mesmas equações dinâmicas que mecânica clássica, mas todos os parâmetros, incluindo as condições iniciais, são dados por números que contém somente uma quantidade finita de informação. Eu não faço nenhuma afirmação metafísica acerca do espaço, do tempo ou dos números, mas ressalto que a matemática usada na prática é sempre finita. Nas seções III-V eu argumento que essa mecânica clássica alternativa é mais natural porque não assume a existência de informação inacessível. Uma forma de se defender a limitação da física a números com informação finita é que qualquer volume finito de espaço pode conter somente uma quantidade finita de informação (ver seção IV). Consequentemente, a imensa evidência empírica da mecânica clássica se aplica igualmente à teoria indeterminística alternativa. A teoria alternativa tem o mesmo (enorme) poder explicativo, seção VI. É, portanto, incorreto dizer que a evidência empírica e o poder explicativo da mecânica clássica sustentam uma visão de mundo determinística, visto que o mesmo corpo de evidências igualmente sustenta uma teoria mecânica clássica alternativa empiricamente equivalente mas indeterminística.
Na segunda parte desse trabalho, eu argumento que toda teoria indeterminística pode ser suplementada por variáveis adicionais de tal modo que ela se torne determinística (da mesma forma como se faz na mecânica bohmiana). Em suma, é suficiente admitir que todo o indeterminismo necessário em um certo ponto do tempo onde, de acordo com a teoria indeterminística, Deus joga os dados, i.e., quando potencialidades tornam-se atuais, poderia ser escondido como variáveis suplementares na condição inicial da teoria determinística equivalente, i.e. Deus jogou todos os dados no big-bang. Isso fecha o círculo: teorias determinísticas são equivalentes a teorias indeterminísticas alternativas em que números reais são substituídos por números de informação finita[3], e teorias indeterminísticas podem ser suplementadas por variáveis adicionais escondidas de tal modo que as teorias suplementadas são determinísticas.
Nas seções VII e VIII a regra elaborada acima para suplementar teorias indeterminísticas é ilustrada na teoria mecânica clássica alternativa e na teoria quântica padrão, levando à mecânica clássica padrão e à mecânica bohmiana, respectivamente. É reconhecido que, nesses dois exemplos, as teorias determinísticas suplementadas têm, além do determinismo, também certa elegância que as favorece. Todavia, pode-se concluir que o determinismo é um preço muito alto a se pagar para aceitar essas variáveis suplementares escondidas. De fato, o indeterminismo explica muito bem, dentre outras coisas, porque ferramentas probabilísticas são tão poderosas na mecânica estatística. Além disso, o indeterminismo abre o futuro, faz das potencialidades um modo real da existência e descreve a passagem do tempo quando as potencialidades se tornam atuais [4, 5].
II. SISTEMAS DINÂMICOS CLÁSSICOS
Os sistemas dinâmicos clássicos mais simples e, no entanto, mais conhecidos são relógios, osciladores harmônicos, dois corpos interagindo via gravidade (por exemplo, um planeta solitário orbitando seu sol) e sistemas similares. Para tais sistemas, as trajetórias são elipses[4] (no espaço ordinário ou de configuração), incluindo os casos de elipses degeneradas, i.e., círculos e linhas retas[5]. Sistemas tão simples como esses são chamados integráveis. Eles se caracterizam por sua estabilidade: a solução em qualquer instante depende tão somente dos principais dígitos da condição inicial. Mais precisamente, uma solução de precisão є depende tão somente da condição inicial descrita com precisão є. Sendo assim, para sistemas tão simples como esses, os dígitos que estiverem muito longe, digamos os que estiverem para lá do bilionésimo dígito, são fisicamente irrelevantes, i.e., não representam nada físico; de maneira retórica, eu escrevo às vezes que esses dígitos que estão muito longe não tem existência física ou não são fisicamente reais.
No entanto, o fato é que quase todos os sistemas dinâmicos clássicos não são integráveis; eles não são simples, mas, pelo contrário, caóticos. Nesse trabalho, à título de clareza, eu considero um sistema dinâmico caótico típico, mas é importante ressaltar que todos os sistemas dinâmicos clássicos não-simples compartilham das características principais de nosso exemplo. Nesse exemplo, nós não consideramos a solução em todos os instantes de tempo, mas somente um conjunto discreto de instantes, digamos cada microssegundo. Além disso, nós assumimos que o sistema está constrangido a permanecer dentro do intervalo de unidades [0…1], i.e., sua coordenada x fica entre 0 e 1. De acordo com isso, sua coordenada pode ser escrita em forma binária como um número tal qual:
(1) x = 0,b1b2b3…bn…
onde os bjs são os dígitos de x em representação binária (equivalentes aos dígitos em base 10). A dinâmica para cada passo de tempo [time step] desse exemplo é dada pelo mapa seguinte:
2x, se x < 1/2
(2) x –>
2x – 1, se x ≥ 1/2
Um tal mapa dinâmico é muito simples de se representar quando a coordenada x é representada em forma binária:
(3) x = 0,b1b2b3…bn…
-> 0,b2b3…bn…
A cada passo de tempo, os bits simplesmente se movem uma posição para a esquerda e o bit principal inicial b1 sai. Depois de n passos de tempo, os bits se movem n passos para a esquerda. Esse exemplo de um sistema caótico genérico é inspirado pelo mapa do padeiro [baker’s map] [6], apesar de que em nosso exemplo há uma descontinuidade em x = 1/2. Note-se, no entanto, que o mapa contínuo do padeiro compartilha todas as características de nosso mapa que são essenciais para nossos argumentos.
Note-se que se o x na equação (1) está na primeira ou na segunda metade da unidade de intervalos é algo completamente determinado pelo bit principal b1. Isso tem a seguinte importante consequência: se o sistema está na primeira ou na segunda metade do intervalo de unidades depois de n passos de tempo é algo determinado pelo primeiro bit depois de n passos de tempo, portanto isso depende do n-ésimo bit da condição inicial.
Um tal sistema caótico ilustra, por exemplo, o desafio das previsões de tempo. Digamos que quando a coordenada x do sistema está do lado esquerdo do intervalo de unidades, isso representa clima chuvoso, enquanto um x do lado direito representa clima ensolarado. Então, o clima durante o tempo de uma semana depende de bits infinitesimais, por exemplo, o bilionésimo bit da condição inicial.
A questão aqui não é a de se esse bilionésimo bit pode ser medido, mas sim se esse bilionésimo bit tem alguma relevância física. Claramente, se as condições iniciais forem definidas por um número real, então esse bilionésimo bit é matematicamente bem definido. Portanto, a questão é se os números matemáticos reais são fisicamente reais.
III. OS NÚMEROS REAIS NÃO SÃO REALMENTE REAIS
O conjunto de todos os números reais é equivalente (isomórfico) ao conjunto de números reais dentro do intervalo unitário. Assim, todos os números relevantes podem ser escritos como em (1), com infinitos bits bj. Essa forma de se escrever os números reais já ilustra o fato de que números reais, em geral, contém uma quantidade infinita de informação (Shannon), i.e., infinitos bits. As únicas exceções são quando a série de bits bj termina, ou mais precisamente quando todos os dígitos depois de uma coordenada finita m são nulos: bj = 0 para todo j > m, ou quando depois de uma posição finita m a série de bits se repete para sempre, como, por exemplo 0,0111011001010101010101010101… que continua com uma repetição sem fim do padrão 01, ou mais genericamente quando há uma fórmula finita (algoritmo) para computar todos os bits.
Uma outra boa forma de ilustrar uma quantidade infinita de informação em números reais típicos se deve a Emile Borel, como bem contado por Greogry Chaitin [7]. Eles enfatizam que um único número real pode conter as respostas para todas as perguntas (binárias) que se possa formular em qualquer linguagem humana. Para se ver isso basta perceber que só há um número finito de linguagens, cada uma com um número finito de símbolos. Assim, pode-se binarizar essa lista de símbolos (como feito rotineiramente nos computadores de hoje em dia) e listar todas as sequências de símbolos, primeiramente as sequências contendo um único símbolo, depois as que contém dois símbolos, e assim por diante. Essa lista imensa de símbolos pode então ser considerada como os bits de um número real. Deixemos 2 bits, bn1bn2, entre cada sequência Sn de símbolos:
(4) 0,S1b11b21S2b21b22S3b31b32…Snbn1bn2…
Quando a sequência Sn de símbolos não representar uma pergunta binária, definimos esses dois bits como 0 (bn1bn2 = 00). Quando eles representam uma pergunta binária cuja resposta é sim, definimos esses bits como 01 e se a resposta é não os definimos como 10. Esse procedimento não é em nada eficiente, mas quem se importa[6]: como um número real tem infinitos bits, não há por que economizar espaço! Assim, pode-se realmente codificar todas as respostas (binárias) possíveis em um único número real. Isso ilustra a quantidade absurdamente ilimitada de informação que números reais podem conter. Números reais são monstros!
Na próxima seção, eu argumento que um volume finito de espaço não pode conter mais que uma quantidade finita de informação. Seguindo essa assunção razoável, eu argumento que os assim chamados números reais não são realmente reais. Mais precisamente, eu argumento que os números matemáticos reais não são fisicamente reais, pelo que eu quero dizer que eles não representam nada físico. De fato, a tese desse trabalho é que toda a física pode ser feita usando somente números de informação finita. Note-se que esses números contém todos os números computáveis, mas não são restritos a eles: eles também contêm “números” cujos dígitos mais distantes são indeterminados, i.e., ainda não determinados[7], como ilustrado na figura 1. Todos os números que contém uma quantidade infinita de informação, eles não podem representar entidades físicas; especificamente, eles não podem ser usados, e de fato não o são, para descrever condições iniciais[8], ver também [9]. Além disso, na prática, nunca se usam números reais, a não ser para provar alguns teoremas não-construtivos de existência gerais e abstratos. O fato de que não se precisa de números reais na prática é bem óbvio, visto que nunca se acessa uma quantidade infinita de informação. Ademais, hoje todas as previsões podem – e na maioria das vezes são – codificadas em computadores, computadores que obviamente carregam uma quantidade finita de bits, como enfatizado na próxima seção. Consequentemente, a física é, na verdade, feita a partir do uso tão somente de números de informação finita e, como veremos na seção VI, a física clássica com condições iniciais de informação finita é uma teoria indeterminística bem definida alternativa à mecânica clássica. Admitidamente, pode-se preferir postular que os números reais são fisicamente significantes, como eu discuto na seção VIII.
IV. UM VOLUME FINITO DE ESPAÇO CONTÉM NO MÁXIMO INFORMAÇÃO FINITA
Aqui eu apresento um argumento que sustenta a colocação de que os números reais não podem representar nada físico. Esse argumento é baseado na assunção de que nenhum volume finito de espaço pode conter uma quantidade infinita de informação. Esse é um resultado bem aceito que se segue do princípio holográfico, conhecido como limite de Bekenstein [10, 11]. Em suma, qualquer armazenamento de um bit de informação requer alguma energia e quantidades suficientemente grandes de energia geram buracos negros. Todavia, para o propósito de minha argumentação, eu acredito que um raciocínio muito mais simples basta para convencer que todo bit de informação ocupa algum espaço, e assim que a densidade de informação é limitada. Deixe-me agora apresentar esse raciocínio baseado em uma assunção intuitiva.
O enorme progresso no armazenamento de informação nas últimas décadas impacta profundamente a nossa sociedade[9]. Hoje, todos sabem que possuem gigabytes de informação em seus bolsos e que companhias como o Google e agências como a NASA armazenam tudo que transita pela internet. Além disso, todos sabem também que cada bit armazenado requer algum espaço. Não muito, possivelmente em breve somente alguns nanômetros cúbicos (10-18 mm3), mas definitivamente um volume finito. Consequentemente, assumindo que informação tem sempre de ser codificada em algo físico, um volume finito de espaço não pode conter mais que uma quantidade finita de informação. Ao menos, isso é uma assunção muito razoável.
Aqui eu gostaria de explorar as consequências teóricas profundas dessa assunção, uma assunção fácil de formular e defender em nossa sociedade baseada na informação, mas uma assunção dificilmente concebível um século atrás. Lembre-se que o conceito moderno de informação foi formalizado por Shannon somente na década de 1940.
Considere um pequeno volume, digamos um centímetro cúbico, contendo uma bola de mármore. Esse pequeno volume pode conter somente uma quantidade finita de informação. Assim, o centro de massa dessa bola de mármore não pode ser um número real (ainda menos 3 números reais), visto que números reais contém – com probabilidade um – uma quantidade infinita de informação. A física clássica descreve o centro de massa da bola através de 3 números reais; e isso é uma descrição extremamente eficiente. Mas a assunção de que um volume infinito de espaço não pode conter mais que uma quantidade finita de informação implica que o centro de massa de qualquer objeto não possa ser identificado com números matemáticos reais. Os números reais são ferramentas úteis, mas são somente ferramentas. Eles não representam a realidade física.
Admitimos que, de acordo com a física de hoje, o argumento acima é um pouco enganador, visto que sabemos que, no final das contas, a bola de mármore e seu centro de massa deveriam ser descritos pela física quântica, incluindo a indeterminação quântica (frequentemente chamada de incerteza). É claro que isso é correto. Mas continuemos com a física clássica porque, primeiro, ela permanece extremamente útil hoje e, segundo, ela é frequentemente apresentada como o arquétipo de teorias determinísticas. O ponto principal desse trabalho é que a física clássica só é determinística se se atribui à ferramenta dos números reais significação física. Assim que se perceber que os números matemáticos reais “não são realmente reais”, i.e., não tem significação física, então se conclui que a física clássica não é determinística, como elaboramos na seção VI. Na verdade, as coisas são ainda piores, como explicamos na próxima seção.
V. NÚMEROS MATEMÁTICOS REAIS SÃO NÚMEROS FÍSICOS ALEATÓRIOS
Alguns números reais podem ser computados até uma precisão arbitrária por um computador, como por exemplo todos os números racionais e números como √2 e π. Tais números computáveis contém somente uma informação finita, o comprimento em bits do menor programa que produz seus dígitos. Note que, visto que só há um número contável de tais programas, o conjunto de números reais que podem ser calculados por um computador é infinitamente menor que o conjunto de todos os números reais. Mais precisamente, o conjunto de números computáveis é infinito-contável, como os inteiros, enquanto o conjunto dos números reais é infinito-contínuo, como os pontos matemáticos de uma linha. Consequentemente, números reais não são computáveis com probabilidade 1. Ou, o que é equivalente, o conjunto de números computáveis tem medida 0 frente ao conjunto dos números reais. Para mais ver [7].
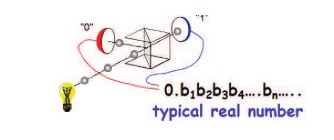
FIG.1: A série de bits de um número real típico é, depois de um certo arranjo inicial de bits, indistinguível de uma sequência de bits verdadeiramente aleatória, como a produzida por um gerador físico de números aleatórios, aqui ilustrado como um gerador quântico de números aleatórios (fótons únicos num divisor de luz seguidos por dois detectores de fótons únicos). Assim, há duas maneiras de se pensar em números reais típicos. A primeira é pensar neles como quantidades dinâmicas: os dígitos muito distantes não têm valor determinado, os valores são produzidos continuamente à medida em que o tempo passa. A segunda é pensar neles como números reais com todos os seus bits dados de início, como se seu valor aleatório tivesse sido produzido em algum tempo inicial. A segunda visão é a padrão, enquanto a primeira é a que defendemos aqui. Note que números computáveis correspondem a geradores de números pseudoaleatórios onde toda a informação está contida na semente finita. Os números de informação finita usados aqui incluem tanto os números computacionais quanto os números dinâmicos reais cujos dígitos muito distantes ainda não estão determinados.
A simples observação que enunciamos acima tem consequências importantes: depois dos primeiros bits, os bits seguintes de todo número real são aleatórios: eles não seguem estrutura alguma. Esses bits são tão aleatórios quanto os resultados das medições quânticas (em meio singleto, digamos), i.e., o mais aleatório possível[10]. Na verdade, não se pode nem mesmo nomear ou caracterizar números reais, visto que há somente uma quantidade contável de números e caracterizações. Assim, quase todos os números reais estão completamente fora de nosso alcance: nós não podemos dizer nada acerca deles, exceto que seus dígitos são aleatórios, que eles não têm estrutura. De fato, se os dígitos de um número real tivessem alguma estrutura, essa estrutura mesma permitiria que se nomeasse a caracterizasse esse número.
De acordo com isso, nomeá-los “números reais” causa uma confusão séria. Uma terminologia melhor seria chamá-los de “números aleatórios”. Infelizmente, Descartes os nomeou “reais” em contraste aos números complexos, aqueles números que incluem a raiz quadrada de -1, tradicionalmente escrita i. Assim:
Números matemáticos reais são números físicos aleatórios.
Eu acredito que se pode especular que, caso houvéssemos aprendido na escola a chamar tais números de “aleatórios” ao invés de “reais”, estaríamos menos inclinados a adotar um ponto de vista determinístico baseado na ciência em que eles figuram.
VI. FÍSICA CLÁSSICA NÃO-DETERMINÍSTICA
Nessa seção retornamos à física, agora que estabelecemos que “os números matemáticos reais são números físicos aleatórios”, i.e., a maioria dos números matemáticos reais são fisicamente imateriais. Nós definimos a mecânica clássica alternativa como composta do mesmo conjunto de equações dinâmicas que a mecânica clássica padrão, mas todos os parâmetros, e de forma notável as condições iniciais, são dados por números de informação finita. Note que para sistemas dinâmicos integráveis, as coordenadas em todos os tempos dadas por um parâmetro de informação finita t são elas mesmas descritas por números de informação finita. Assim, todas as previsões sobre sistemas integráveis se mantêm inalteradas.
No entanto, voltando ao exemplo do sistema dinâmico clássico caótico típico da seção II, nós lembramos que o primeiro bit do sistema, i.e., o bit que determina se o sistema está na metade esquerda (clima chuvoso) ou na metade direita do intervalo de unidade (clima ensolarado) depois de n passos de tempo, depende do n-ésimo bit da condição inicial bn. Mas, se n for grande o suficiente, esse n-ésimo bit da condição inicial não teria, no tempo correspondente à condição inicial, nenhuma significação física. Assim, de acordo com a nossa mecânica clássica alternativa, sistemas dinâmicos caóticos são verdadeiramente aleatórios. Deixe-me enfatizar que eles não são somente aleatórios para todo propósito prático, mas sim verdadeiramente aleatórios, tão aleatórios quanto os resultados de medições quânticas. Essa aleatoriedade não tem nada a ver com limitações tecnológicas, ela é aleatoriedade pura e intrínseca.
Essa visão que estou sugerindo é a de que os primeiros bits na expressão de x são “realmente reais” (e.g., no presente, está realmente ou fazendo sol ou chovendo), enquanto os bits muito distantes são totalmente aleatórios. À medida em que o tempo passa, eles são deslocados para a esquerda, uma posição a cada passo de tempo[11]. Assim, eles adquirem um valor definido passo a passo. À medida em que o tempo passa, eles têm uma disposição (ou propensão) diferente a manter seu valor eventual. Essa propensão muda a cada passo de tempo, de maneira similar ao movimento browniano de alguma partícula que permanece entre duas placas grudentas (de valores 0 e 1) até que eventualmente ela gruda em alguma das duas[12]. De acordo com isso, a abertura do futuro entra gradualmente, às vezes em escalas de milissegundo e em outros sistemas em escalas de milhões de anos. Isso é só a breve colocação de uma ideia, uma elaboração será desenvolvida em um trabalho futuro.
Pode-se objetar que essa visão é arbitrária, já que não há nenhum número natural onde a transição de bits determinados para bits aleatórios aconteça. Isso é correto, apesar de não ser importante na prática enquanto essa transição está nas séries de bits mais distantes. A falta de uma transição natural é devido ao fato de que, na física clássica, não há nada equivalente à constante de Planck da teoria quântica. Mas isso é muito natural, visto o fato ser que quando se olha para essa transição na descrição física de sistemas clássicas, chega-se na física quântica.
Admitidamente, as equações de Newton, assim como as equações de Maxwell, são determinísticas: dadas as condições iniciais sob a forma de números reais, todo o futuro e passado está fixado [13]. Mas o fato é que essas equações serem matematicamente determinísticas não implica que a física é determinística. Por exemplo, isso definitivamente não é o caso quando as condições iniciais de sistemas caóticos não são identificáveis com números matemáticos reais, como na nossa mecânica clássica alternativa. Consequentemente, se a física clássica é ou não determinística não é uma questão científica, mas depende da significação física que se associa com os números matemáticos reais.
Como a filósofa Elizabeth Anscombe enfatizou [14], “o grande sucesso da astronomia newtoniana foi, em um certo nível, um desastre intelectual: ele produziu uma ilusão […] pois isso deu a impressão de que nós tínhamos aqui um ideal de explicação científica; enquanto a verdade era que foi só a prestatividade do sistema solar, que teve uma história tão pacífica durante o tempo registrado, que forneceu esse modelo”.
VII. VARIÁVEIS SUPLEMENTARES…
Até agora vimos que a física é não-determinística e que isso é verdade tanto para a mecânica quântica quanto para a mecânica clássica alternativa. Nessa seção, nós nos voltamos para a questão natural de se se pode adicionar variáveis suplementares às mecânicas quântica e clássica alternativa para restaurar o determinismo.
Que isso é possível no caso da mecânica clássica já é bem conhecido. É suficiente adicionar os números matemáticos reais, como é usualmente feito sem sequer se mencionar que eles são variáveis suplementares. Uma vez que números reais são adicionados e postulados como sendo parte da ontologia da teoria, a teoria estendida é determinística. De alguma forma, toda a aleatoriedade foi colocada nas (inalcançáveis) condições iniciais, como discutido na próxima seção.
Para os físicos isso pode parecer uma piada: nós primeiro argumentamos que “os números reais não são realmente reais” só para depois introduzi-los novamente. Mas note-se aquilo que é atingido quando se toma as coisas dessa forma. Os números reais certamente não são parte necessária da ontologia da física clássica, não são os fatos experimentais que forçam a física a incluir os números reais na ontologia da física clássica. Assim, de começo, a física clássica é não-determinística. No entanto, toda teoria não-determinística pode se tornar determinística pela adição de variáveis suplementares. De forma absolutamente genérica, seria suficiente, por exemplo, adicionar como variáveis suplementares todos os resultados de todas as medições futuras, enquanto se garante que todas essas variáveis suplementares permanecem escondidas até que as medições correspondentes tenham ocorrido. Na verdade, é exatamente assim que a mecânica clássica é feita: postular que a condição inicial de todo sistema dinâmico clássico é descrita fielmente por números reais é uma forma elegante de se adicionar todos os resultados futuros, ao mesmo tempo em que se garante que eles permaneçam inacessíveis por tempo suficiente. Admitidamente, só adicionar resultados futuros e postular que eles são inacessíveis não irá convencer nenhum cientista. Adicionar os números reais à física clássica é muito mais convincente, porque é elegante. Mas é realmente diferente?
E a física quântica? Aqui há uma maneira bem conhecida de adicionar variáveis suplementares de forma a tornar a mecânica quântica determinística. Isso é conhecido como mecânica bohmiana (ou interpretação de Broglie-Bohm) [16-18]. Essencialmente, postula-se que todas as partículas sempre têm posições bem definidas – apesar de inacessíveis -, e que, no fim das contas, todas as medições são medições de posição (posição de um ponteiro, posição de elétrons que ligam/desligam um LED etc.). Essas posições de partículas, que eu nomeio posições bohmianas, são guiadas pela solução da equação usual de Schrödinger de uma forma inteligente tal que, se se assume que as posições inicias são distribuídas estatisticamente de acordo com a probabilidade quântica, i.e., |ψ(x)|2, então a distribuição estatística das posições bohmianas permanece em acordo com as probabilidades quânticas a todo momento. Isso é muito elegante e, como para os números reais na física clássica, adicionar posições bohmianas à ontologia da teoria transforma a física quântica em uma teoria determinística. Note-se que é necessário também “confiar” nos números reais, do modo como as posições bohmianas e o vetor de estado quântico os utilizam.
Uma certa precaução é necessária aqui: no caso de sistemas compostos de mais de uma partícula, deve-se perceber que a evolução de qualquer partícula, digamos a primeira, depende da função de onda inteira. Assim, depende também daquilo que acontece na localização das outras partículas, i.e., cada partícula é guiada de maneira não-local. Isso é necessário porque as previsões quânticas violam o teorema de Bell, e sendo assim toda teoria alternativa (ou suplementada) que reproduza as previsões quânticas devem conter algumas características não-locais [15, 19, 20]. Mas é provavelmente por isso que a maioria dos físicos rejeita a mecânica bohmiana: eles não gostam da não-localidade explícita (apesar de inevitável).
VIII. …TRANSPORTAM A ALEATORIEDADE PARA A CONDIÇÃO INICIAL
Como vimos na seção anterior, tanto o não-determinismo quântico quanto o clássico alternativo podem se tornar determinísticos pela adição de variáveis suplementares. Em ambos os casos, a teoria determinística complementada é bem elegante. Em ambos os casos, a aleatoriedade original é transportada para a condição inicial. De fato, à medida em que o tempo passa, ao invés de novos bits na série inicial (1) ganharem valores determinados, novos bits da condição inicial ganham relevância. Assim, nos confrontamos com uma escolha: ou o fato de que, no presente, algumas coisas acontecem e outras não é interpretado como revelação, retroativa, de informação acerca de condições iniciais já há muito tempo passadas, ou então nós entendemos o presente como resultado de uma realidade indeterminada, e o futuro como aberto. Se nos importarmos com como nós experimentamos a realidade, a segunda opção é obviamente a melhor.
É digno de nota que quase todos os físicos complementam a mecânica clássica alternativa com números matemáticos reais; e o fazem sem nem mesmo pensar sobre isso. Ao mesmo tempo, quase todo físico rejeita a mecânica bohmiana argumentando que ela é desnecessariamente complicada e que não leva a uma nova física. No entanto, pode-se argumentar que os números reais aceitos pela física clássica são também desnecessariamente complicados (lembremos, eles contêm uma quantidade infinita de informação. Não é isso imensamente complexo?). Além disso, pode-se perguntar qual nova física os números reais produziram.
IX. CONCLUSÃO
Em nossa sociedade, o conceito de informação é onipresente. Hoje é muito natural assumir que nenhum volume finito de espaço pode conter mais que uma quantidade finita de informação (Shannon), medida por bits. Consequentemente, eu argumento que não se deve atribuir aos números reais, i.e., a números que contém uma quantidade infinita de informação, nenhuma significação física. Essa observação implica que há uma alternativa simples à mecânica clássica padrão, baseada em números de informação finita, que é uma teoria não-determinística, apesar de ter exatamente o mesmo poder de previsão e explicação.
No tempo de Laplace, o conceito de informação, particularmente sua quantização em termos de bits, não existia. Assim, era natural identificar condições iniciais de sistemas dinâmicos clássicos com os números matemáticos reais. Mas agora que sabemos que os “números reais” contém uma quantidade infinita de informação e que, como sugerimos acima, eles deveriam ser chamados de “números aleatórios”, devíamos perceber que tais números não podem ser a base para o determinismo.
De acordo com isso, ambas as teorias clássica e mecânica podem e, eu apelo, devem ser vistas como não-determinísticas. É claro que se pode querer complementar essas teorias com variáveis suplementares de tal modo que a teoria complementada é determinística. Note-se que isso pode ser feito tanto para a física clássica quanto para a física quântica, como visto nas seções VII e VIII; em ambos os casos as variáveis suplementares são inacessíveis. O fato é que a maioria dos físicos facilmente complementa a física clássica, mas é relutante em fazer o mesmo para a física quântica.
Em suma, a física – com todo seu poder de previsão e explicação – pode ser apresentada como intrinsecamente não-determinística. A visão dominante de acordo com a qual a física clássica é determinística é devida, primeiramente, a uma falsa impressão gerada pelo seu grande sucesso na astronomia e na concepção de relógios e outros sistemas mecânicos simples (integráveis) e, também, pela falta de apreciação de suas implicações para densidade de informação (infinita).
Finalmente, um mundo indeterminístico é acolhedor para a Res Potentia e para a passagem do tempo [22, 23, 25].
Reconhecimento
Esse trabalho é fruto de discussões estimulantes com Augustin Baas, Cyril Branciard, Barbara Drossel, Florian Fröwis, Michael Hall, John Norton, Valerio Scarani e Christian Wüthrich. O suporte financeiro dado ERC-AG MEC europeu é reconhecido e gratificado.
[1] J.D. Norton, www.pitt.edu/∼jdnorton/Goodies/Dome
[2] Y. Dolev, Relativity, Global Tense and Phenomenology, in Cosmological and Psychological Time, Y. Dolev and M. Roubach Eds., Springer, Boston Studies in the Philosophy of Science (2016).
[3] B. Drossel, On the relation between the second law of thermodynamics and classical and quantum mechanics, arXiv:1408.6358
[4] J. Norton, Time Really Passes, Journal of Philosophical Studies 13, 23-34 (2010).
[5] Y. Dolev, Physics’ silence on time, Euro. Jnl. Phil. Sci., https://doi.org/10.1007/s13194-017-0195-z (2018).
[6] https://en.wikipedia.org/wiki/Baker%27s map
[7] G. Chaitin, The Labyrinth of the Continuum, in Meta Math!, Vintage Books, NY, 2008.
[8] C.J. Posy, Varieties of Indeterminism in the Theory of General Choice Sequences, J. Philosophical Logic 5, 91-132 (1976).
[9] G. Dowek, Real numbers, chaos and the principle of a bounded density of information, Computer Science – Theory and Applications, pp 347-353 (2013).
[10] R. Bousso, The holographic principle, Rev. Mod. Phys. 74, 825 (2002).
[11] J.D. Bekenstein, Universal upper bound to entropy-toenergy ratio for bounded systems, Phys.Rev. D 23, 287-298 (1981)
[12] M. Dorato, Do Dispositions and Propensities have a role in the Ontology of Quantum Mechnanics? Some Critical Remarks, in Probabilities, Causes and Propensities in Physics, Ed. M. Su´arez, Synthese Library, Springer, pp 197-218 (2011).
[13] N. Gisin and I.C. Percival, J. Phys. A, 25, 5677 (1992).
[14] G.E.M. Anscombe, Inaugural lecture at Cambridge University on Causality and Determination, 1971.
[15] N. Gisin, Quantum Chance, nonlocality, teleportation and other quantum marvels, Springer, 2014.
[16] D. Bohm, A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables, Phys. Rev., 85, 166 and 180, (1952).
[17] J.S. Bell, On the Impossible Pilot Wave, Found. Phys. 12, 989-999 (1982).
[18] D. D¨urr and S. Teufel, Bohmian mechanics: the physics and mathematics of quantum theory, Springer Science & Business Media (2009).
[19] J. S. Bell, Speakable and Unspeakable in Quantum Mechanics: Collected papers on quantum philosophy (Cambridge University Press, Cambridge, 1987).
[20] N. Brunner, D. Cavalcanti, S. Pironio, V. Scarani, S. Wehner, “Bell nonlocality,” Rev. Mod. Phys. 86, 419 (2014).
[21] N. Gisin, Propensities in a non-deterministic physics, Synthese 98, 287 (1991).
[22] N. Gisin, Time really Passes, Science can’t deny that, arxiv/1602.01497, in Time in Physics, eds R. Renner and S. Stupar, Springer 2017.
[23] Admitidamente, o não-determinismo de nossa mecânica clássica alternativa questiona quando é que as potencialidades devêm atuais. Continuamente como parte da dinâmica [24]? Isso pode lançar nova luz sobre o antigo e infame problema da “medição” quântica. Também questões sobre a reversão do tempo podem ter respostas interessantes. Se se inverte o mapa (3), novos primeiros bits têm de ser adicionados a cada passo de tempo, mas sem perder nenhum bit. Assim, tanto o futuro quanto o passado são abertos, mas o presente contém mais informação sobre o passado do que sobre o futuro.
[24] N. Gisin, Collapse. What else? arXiv:1701.08300, published in Collapse of the Wave Function, Cambridge University Press, ed. Shan Gao, pp 207-224, 2018.
[25] Y. Dolev, Motion and Passage – The Old B-Theory and Phenomenology, in Debates in the Metaphysics of Time, Oaklander L. N, Editor, Bloomsbury, 2014.
[1] Como, por exemplo, o domo de Norton [1] e colisões frontais de partículas pontuais.
[2] Aqui, indeterminística é tão somente a negação de determinística, i.e, sinônimo de não-determinística: o presente e as leis da natureza estando dadas, há mais de um futuro possível.
[3] Como explicado nas seções III e IV, ver também Fig.1, os números de informação finita contém todos os números computáveis, mas não se restringem a eles.
[4] Trajetórias cujas coordenadas são senos e cossenos, funções que todo computador “sabe” calcular de forma eficiente.
[5] Ou as trajetórias escapam para o infinito seguindo parábolas ou hipérboles.
[6] Um código ainda mais econômico poderia ignorar todas as sequências de símbolos que não representam nenhuma questão e adicionar, depois de cada questão significativa, um cógido de um único bit para a resposta.
[7] Isso é, de certa forma, reminiscente dos números indeterminados de Brouwer.
[8] Para ser claro – eu não estou fazendo colocações pertinentes à natureza dos números, ou assunções referentes à realidade ou irrealidade dos números. Minha preocupação é a de distinguir os números que tem significação física daqueles que não tem. Nem estou eu, em absoluto, preocupado com a bem-conhecida e assustadora tarefa de prestar contas acerca da aplicabilidade da matemática à ciência. Finalmente, eu não estou argumentando contra o uso dos números reais como uma ferramente útil ao cálculo, simplesmente só números de informação finita podem representar algo físico.
[9] Permita-me um parêntese. O enorme progresso no armazenamento de informação e o progresso relativamente pequeno no armazenamento de energia explica porque a ficção científica de um século atrás não pode absolutamente prever a “revolução da internet”. Na ficção científica daqueles dias ninguém podia ter uma enciclopédia no bolso, mas todos estavam voando graças a pequenas mochilas.
[10] Uma certa precaução é necessária aqui, visto que nem todos os bits de todos os números reais são aleatórios, como ilustrado no exemplo seguinte. Define-se um número com todos os bits em posições pares sendo idênticos ao bit correspondente do número computável π, e todos os bits em posições ímpares determinados pelos resultados sucessivos de uma dada sequência (infinita) de “verdadeiros lances de dados”, e.g. os resultados de um gerador quântico de números aleatórios. Em tal caso artificial, todo segundo bit é previsível, mas todos os outros são verdadeiramente aleatórios.
[11] Os passos de tempo são usados aqui somente como ilustração. O tempo poderia passar muito mais devagar, com a propensão de todos os bits variando devagar.
[12] Note-se que isso é similar ao estado quântico de um bit-quântico (qubit) em modelos de localização espontânea descritos pelas equações estocásticas de Schrödinger [13].
[13] Para casos excepcionais, ver a nota 1.
Texto original: https://link.springer.com/article/10.1007/s10670-019-00165-8
Traduzido por: Pedro Naccarato
Revisado por: Marcus Apolinário


